Makine Öğrenmesi’nde backpropagation gibi öğrenme algoritmalarında sonuç bulunur ve hata geriye doğru işletilerek minimize edilmeye çalışılır. Hatanın geriye doğru işlemesini sağlamak için girdi (input) değerlerine göre kısmi türevler alınır. Sonucun (hatanın) girdilere göre alınmış kısmi türevlerine özel olarak gradyan deniyor.
Bilindiği gibi hatayı minimize etmek aslında bir optimizasyon meselesidir. Geçen yazılarımızdan birinde hatayı (cost) bulduktan sonra en aza çekebilmek için bir arama (search) işleminin yapıldığından bahsetmiştik. Bu arama \(\theta\) ile \(J(\theta)\) ikili uzayında yapılır ve \(J(\theta)\)‘nın \(\theta\)‘ya göre değişimine bakılır. Bu arama işi, temel olarak en küçük \(J(\theta)\) değerinin “bir şekilde” saklanmasıyla ya da en küçük değerinin aranıp bulunmasıyla olabilir, ancak milyonluk ya da milyarlık bir dizide arama yapmanın maliyeti çok yüksektir. Bu yüzden türev alma tekniğiyle matematiksel olarak \(J(\theta)\)‘nın en küçük değeri bulunur.
Backpropagation algoritması temel olarak 3 işlev barındırır. 1. Sonucu hesaplamak için forward işlemi, 2. Hatayı geriye doğru işletmek (backward) için gradyan alma işlemi, 3. Gradient Descent [1] gibi [2][3] bir optimizasyon algoritmasıyla parametrelerin güncellenmesi. Bu yazıda temel düzey hesaplarla gradyan alma işlemini tanıtacağız.
Gradyan başta da söylediğimiz gibi kısmi türevlerin alınmasından başka bir şey değil. Toplama, çarpma gibi işlemleri kapılarla yaptığımızı düşünürsek bir devre üzerinde bulunan bütün kapıların diğer kapılardan bağımsız olarak gerçekleştirdiği iki işlem vardır: 1. Gelen girdiyi hesaplayıp sonucu bulmak, 2. Girdilerin sonuca göre yerel gradyanlarını bulmak. Her kapı bu iki işlemi diğer kapılardan bağımsız olarak, diğerlerinden habersiz olarak yapar. Bulunan yerel gradyanlar, devre üzerindeki yolu (path) izlenerek geriye doğru birbiriyle çarpılır ve devre üzerindeki global gradyanlar bulunmuş olur. Basit olarak çatallanmış (branch) gradyanlar toplanırken, seri bir yol üzerinde olan gradyanlar çarpılırlar.
Bir fonksiyonun gradyanını almak, değişkenlerin fonksiyon sonucuna ne düzeyde etki ettiğini bulmaya yarar. Örneğin: \(f(x,y)\;=\;xy\) gibi bir fonksiyonda \(x\) değişkeninin \(f(x,y)\) fonksiyonuna nasıl etki ettiği; \(f\)‘in \(x\)‘e göre kısmi türevi alınarak bulunur:
$$\frac{\partial f}{\partial x}\;=\;y$$
Bu demektir ki, \(x\)‘in sonuca etkisi \(y\)‘nin değerine bağlıdır. Aynı şekilde:
$$\frac{\partial f}{\partial y}\;=\;x$$
Kısmi türevinden görüleceği gibi \(y\)‘nin de sonuca etkisi \(x\)‘in değerine bağlıdır. \((3,-2)\) değerlerine sahip bir \(f\) fonksiyonunda; \(x\)‘in kısmisi \(-2\) olurken, \(y\)‘nin kısmisi \(3\) olacaktır. Peki bu gradyanlar bu fonksiyon için ne anlama gelir? \(\underset{h\rightarrow0}{lim}\) iken \(x\) değeri, \(h\) değeri kadar arttırılırsa, fonksiyonun sonucu \(2h\) kadar azalır, ya da tam tersi; \(x\) değeri, \(h\) kadar azaltılırsa, fonksiyonun sonucu \(2h\) kadar artar. \(x\)‘in kısmisinin önündeki negatiflik \((-2)\) bu zıtlığı göstermektedir.
Devre üzerindeki yerel gradyanları teker teker çarpmak aslında kısmi türevde zincir kuralının devre sonundan başına doğru uygulanmasından başka bir şey değildir.
Gradyanları kolaylıkla bulmak için önerilen bir yöntem vardır. Otomatik türev alma adı verilen yöntemle karmaşık fonksiyonlar küçük fonksiyonlara bölünür ve bu fonksiyonların sonucu ara değişkenlerde tutulur. Bu ara değişkenlerse diğer fonksiyonlarda bir değişken gibi işlev görür. Bu yöntemi bir örnekle açıklayalım:
$$f(x,y,z)\;=\:(x+y)z$$
üç değişkenli fonksiyonumuz olsun.
$$h\;=\;x+y$$
eşitliğiyle \((x + y)\) sonucunu bir ara değişkende tutarsak,
$$f(h,z)\;=\:hz$$
gibi bir fonksiyon elde ederiz. Böylelikle \(f(x,y,z)\) fonksiyonu, toplama ve çarpmadan oluşan ayrı fonksiyonlar halinde düşünülerek yerel gradyanlar alınır ve daha sonra zincir kuralı uygulanabilir. Peki, o halde yukarıdaki fonksiyonun yerel gradyanlarını almaya başlayalım:
$$f(h,z)\;=\:hz$$
$$\frac{\partial f}{\partial h}=z\;\;\;ve\;\;\;\frac{\partial f}{\partial z}=h$$
Buradan \(f\)‘in \(x\)‘e göre kısmisi:
$$\begin{array}{l}\frac{\partial f}{\partial x}=\frac{\partial f}{\partial h}\cdot\frac{\partial h}{\partial x}\\\frac{\partial f}{\partial h}=z,\;\;\;\;\frac{\partial h}{\partial x}=1\;\;\;\;ise;\\\frac{\partial f}{\partial x}=z\cdot1\;=z\end{array}$$
olarak bulunur. Ara değişken kullanmadan \(f\) fonksiyonunun \(x\)‘e göre kısmisi alınırsa:
$$\begin{array}{l}f(x,y,z)=(x+y)z\\f(x,y,z)=xz+yz\\\end{array}$$
Buradan \(f\)‘in \(x\)′e kısmisi alındığında \(z\)′yi sabit olarak düşünebiliriz. O halde;
$$\frac{\partial f}{\partial x}=z$$
olduğu görülür. Bu fonksiyonun kısmi türevlerini bulmak kolaydır ancak fonksiyon karmaşıklaştıkça gradyanlarını bulmak hem zor hem de zaman alıcı olacaktır. Bu yüzden karmaşık fonksiyonların gradyanlarını bulmak için aradeğişkenler kullanılır ve bu aradeğişkenlerin gradyanlarına zincir kuralı uygulanarak çarpılır ve global gradyan bulunmuş olur.
Fonksiyonları temel olarak toplama, çarpma ve max işlemlerine (fonksiyonlarına) dönüştürerek ifade edebiliriz. Bu işlemler makine öğrenmesi algoritmalarında sıkça kullanılırlar. Bu fonksiyonlar ve yerel gradyanları devre üzerinde nasıl gösterilir, verip bitirelim.
Çarpma:
$$f(x,y)=xy,\;\;\;\;\;\frac{\partial f}{\partial x}=y,\;\;\;\;\;\frac{\partial f}{\partial y}=x$$
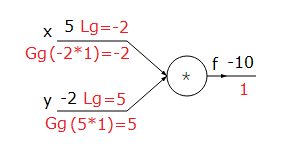 |
| Şekil-1. Çarpma fonksiyonu |
Toplama:
$$f(x,y)=x+y,\;\;\;\;\;\frac{\partial f}{\partial x}=1,\;\;\;\;\;\frac{\partial f}{\partial y}=1$$
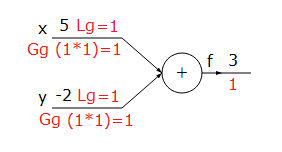 |
| Şekil-2. Toplama fonksiyonu |
Max (Maximum alma):
$$f(x,y)=\underset{(x>y)}{max(x,y)},\;\;\;\;\frac{\partial f}{\partial x}=1,\;\;\;\;\;\frac{\partial f}{\partial y}=0$$
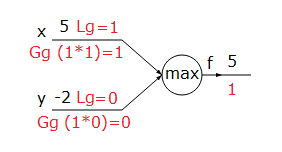 |
| Şekil-3. Max fonksiyonu |
Şekillerin üzerindeki kırmızıyla yazılanlar gradyanları göstermektedir. Lg yerel gradyan, Gg global gradyan anlamında kullanılmıştır.
[1] Gradient Descent
[2] Stochastic Gradient Descent
[3] Mini-Batch Gradient Descent